Description

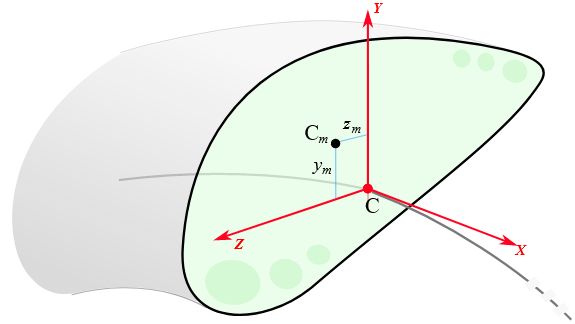
Inertia properties of a beam of Cosserat type, not necessarily of uniform density, from the following information that allows the center of mass to be offset respect to the beam centerline:

a mass per unit length
offset of the center of mass Cm along Y Z section axes,
Jyy Jzz Jzy moments of inertia computed in section reference Y Z, not rotated and origin in centerline The polar moment of area is automatically inferred via perpendicular axis theorem.

#include <ChBeamSectionCosserat.h>

Inheritance diagram for chrono::fea::ChInertiaCosseratAdvanced:

[legend]

Collaboration diagram for chrono::fea::ChInertiaCosseratAdvanced:

[legend]

Public Member Functions
	ChInertiaCosseratAdvanced (double mu_density, double c_y, double c_z, double Jyy_moment, double Jzz_moment, double Jyz_moment)

	ChInertiaCosseratAdvanced (double mu_density, double c_y, double c_z, ChVector3d Ivals)

virtual void	ComputeInertiaMatrix (ChMatrix66d &M) override
	Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mi]{xvel,wvel} The matrix is computed in the material reference.

virtual void	ComputeInertiaDampingMatrix (ChMatrix66d &Ri, const ChVector3d &mW) override
	Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]d{xacc,wacc}+[Ri]d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference. More...

virtual void	ComputeInertiaStiffnessMatrix (ChMatrix66d &Ki, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc) override
	Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]d{xacc,wacc}+[Ri]d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference. More...

virtual void	ComputeQuadraticTerms (ChVector3d &mF, ChVector3d &mT, const ChVector3d &mW) override
	Compute the values of inertial force & torque depending on quadratic velocity terms, that is the gyroscopic torque w x [J]w and the centrifugal term (if center of mass is offset). More...

virtual double	GetMassPerUnitLength () override
	Get mass per unit length, ex.SI units [kg/m].

virtual void	SetMassPerUnitLength (double mmu)
	Set mass c, ex.SI units [kg/m]. More...

void	SetCenterOfMass (double my, double mz)
	"mass reference": set the displacement of the center of mass respect to the section centerline reference.

double	GetCenterOfMassY ()

double	GetCenterOfMassZ ()

virtual void	SetInertiasPerUnitLength (double Jyy_moment, double Jzz_moment, double Jyz_moment)
	Set inertia moments, assumed computed in the Y Z unrotated reference frame of the section at centerline, and defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), also Jyy = Mm(4,4) \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), also Jzz = Mm(5,5) \( J_{yz} = \int_\Omega \rho y z d\Omega \), also Jyz = -Mm(4,5) = -Mm(5,4) Note that for an uniform density, these are also related to second moments of area as \( J_{yy} = \rho I_{yy} \), \( J_{zz} = \rho I_{zz} \). More...

virtual double	GetInertiaJxxPerUnitLength ()
	Get the Jxx component of the inertia per unit length (polar inertia), in the Y Z unrotated reference frame of the section at centerline. More...

virtual double	GetInertiaJyyPerUnitLength ()
	Get the Jyy component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline, also Jyy = Mm(4,4)

virtual double	GetInertiaJzzPerUnitLength ()
	Get the Jzz component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline, also Jzz = Mm(5,5)

virtual double	GetInertiaJyzPerUnitLength ()
	Get the Jyz off-diagonal component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline. More...

virtual void	SetMainInertiasInMassReference (double Jmyy, double Jmzz, double phi)
	Set inertia moments, per unit length, as assumed computed in the Ym Zm "mass reference" frame, ie. More...

virtual void	GetMainInertiasInMassReference (double &Jmyy, double &Jmzz, double &phi)
	Get inertia moments, per unit length, as assumed computed in the Ym Zm "mass reference" frame, and the rotation phi of that frame, ie. More...

Public Member Functions inherited from chrono::fea::ChInertiaCosserat
virtual void	ComputeInertialForce (ChVector3d &mFi, ChVector3d &mTi, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc)
	Compute the total inertial wrench, ie forces and torques (per unit length). More...

Additional Inherited Members
Public Attributes inherited from chrono::fea::ChInertiaCosserat
ChBeamSectionCosserat *	section

bool	compute_inertia_damping_matrix = true
	Flag that turns on/off the computation of the [Ri] 'gyroscopic' inertial damping matrix. More...

bool	compute_inertia_stiffness_matrix = true
	Flag that turns on/off the computation of the [Ki] inertial stiffness matrix. More...

bool	compute_Ri_Ki_by_num_diff = false
	Flag for computing the Ri and Ki matrices via numerical differentiation even if an analytical expression is provided. More...

Constructor & Destructor Documentation

◆ ChInertiaCosseratAdvanced() [1/2]

chrono::fea::ChInertiaCosseratAdvanced::ChInertiaCosseratAdvanced	(	double	mu_density,
		double	c_y,
		double	c_z,
		double	Jyy_moment,
		double	Jzz_moment,
		double	Jyz_moment
	)

inline

Parameters

mu_density	mass per unit length [kg/m]
c_y	displacement of center of mass along Y
c_z	displacement of center of mass along Z
Jyy_moment	moment of inertia per unit length, about Y. Jyy=Mm(4,4)
Jzz_moment	moment of inertia per unit length, about Z. Jzz=Mm(5,5)
Jyz_moment	moment of inertia per unit length, about YZ (off diagonal term). Jyz=-Mm(4,5)=-Mm(5,4)

◆ ChInertiaCosseratAdvanced() [2/2]

chrono::fea::ChInertiaCosseratAdvanced::ChInertiaCosseratAdvanced	(	double	mu_density,
		double	c_y,
		double	c_z,
		ChVector3d	Ivals
	)

inline

Parameters

mu_density	mass per unit length [kg/m]
c_y	displacement of center of mass along Y
c_z	displacement of center of mass along Z
Ivals	moments of inertia

Member Function Documentation

◆ ComputeInertiaDampingMatrix()

void chrono::fea::ChInertiaCosseratAdvanced::ComputeInertiaDampingMatrix	(	ChMatrix66d &	Ri,
		const ChVector3d &	mW
	)

overridevirtual

Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference.

Parameters

Ri	6x6 sectional inertial-damping (gyroscopic damping) matrix values here
mW	current angular velocity of section, in material frame

Reimplemented from chrono::fea::ChInertiaCosserat.

◆ ComputeInertiaStiffnessMatrix()

void chrono::fea::ChInertiaCosseratAdvanced::ComputeInertiaStiffnessMatrix	(	ChMatrix66d &	Ki,
		const ChVector3d &	mWvel,
		const ChVector3d &	mWacc,
		const ChVector3d &	mXacc
	)

overridevirtual

Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference.

NOTE the matrix already contains the 'geometric' stiffness, so it transforms to absolute transl/local rot just like [Mi] and [Ri]: [Ki]_al =[R,0;0,I]*[Ki^]*[R',0;0,I'] , with [Ki^]=([Ki]+[0,f~';0,0]) for f=current force part of inertial forces.

Parameters

Ki	6x6 sectional inertial-stiffness matrix [Ki^] values here
mWvel	current angular velocity of section, in material frame
mWacc	current angular acceleration of section, in material frame
mXacc	current acceleration of section, in material frame (not absolute!)

Reimplemented from chrono::fea::ChInertiaCosserat.

◆ ComputeQuadraticTerms()

void chrono::fea::ChInertiaCosseratAdvanced::ComputeQuadraticTerms	(	ChVector3d &	mF,
		ChVector3d &	mT,
		const ChVector3d &	mW
	)

overridevirtual

Compute the values of inertial force & torque depending on quadratic velocity terms, that is the gyroscopic torque w x [J]w and the centrifugal term (if center of mass is offset).

All terms expressed in the material reference, ie. the reference in the centerline of the section.

Parameters

mF	centrifugal term (if any) returned here
mT	gyroscopic term returned here
mW	current angular velocity of section, in material frame

Implements chrono::fea::ChInertiaCosserat.

◆ GetInertiaJxxPerUnitLength()

virtual double chrono::fea::ChInertiaCosseratAdvanced::GetInertiaJxxPerUnitLength ( )

inlinevirtual

Get the Jxx component of the inertia per unit length (polar inertia), in the Y Z unrotated reference frame of the section at centerline.

Note: it automatically follows Jxx=Jyy+Jzz for the polar theorem.

◆ GetInertiaJyzPerUnitLength()

virtual double chrono::fea::ChInertiaCosseratAdvanced::GetInertiaJyzPerUnitLength ( )

inlinevirtual

Get the Jyz off-diagonal component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline.

Also Jyz = -Mm(4,5) = -Mm(5,4)

◆ GetMainInertiasInMassReference()

void chrono::fea::ChInertiaCosseratAdvanced::GetMainInertiasInMassReference	(	double &	Jmyy,
		double &	Jmzz,
		double &	phi
	)

virtual

Get inertia moments, per unit length, as assumed computed in the Ym Zm "mass reference" frame, and the rotation phi of that frame, ie.

inertias centered at the center of mass and rotated by phi angle to match the main axes of inertia: \( Jm_{yy} = \int_\Omega \rho z_{m}^2 d\Omega \), \( Jm_{zz} = \int_\Omega \rho y_{m}^2 d\Omega \). Assuming the center of mass is already set.

Reimplemented in chrono::fea::ChInertiaCosseratMassref.

◆ SetInertiasPerUnitLength()

void chrono::fea::ChInertiaCosseratAdvanced::SetInertiasPerUnitLength	(	double	Jyy_moment,
		double	Jzz_moment,
		double	Jyz_moment
	)

virtual

Set inertia moments, assumed computed in the Y Z unrotated reference frame of the section at centerline, and defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), also Jyy = Mm(4,4) \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), also Jzz = Mm(5,5) \( J_{yz} = \int_\Omega \rho y z d\Omega \), also Jyz = -Mm(4,5) = -Mm(5,4) Note that for an uniform density, these are also related to second moments of area as \( J_{yy} = \rho I_{yy} \), \( J_{zz} = \rho I_{zz} \).

Note also that \( J_{xy} = J_{xz} = J_{yx} = J_{zx} = 0 \) anyway. Note also that \( J_{xy} \) does not need to be input, as automatically computed via \( J_{xx} = J_{yy} +J_{zz} \) for the polar theorem.

Reimplemented in chrono::fea::ChInertiaCosseratMassref.

◆ SetMainInertiasInMassReference()

void chrono::fea::ChInertiaCosseratAdvanced::SetMainInertiasInMassReference	(	double	Jmyy,
		double	Jmzz,
		double	phi
	)

virtual

Set inertia moments, per unit length, as assumed computed in the Ym Zm "mass reference" frame, ie.

centered at the center of mass and rotated by phi angle to match the main axes of inertia: \( Jm_{yy} = \int_\Omega \rho z_{m}^2 d\Omega \), \( Jm_{zz} = \int_\Omega \rho y_{m}^2 d\Omega \). Assuming the center of mass is already set.

Reimplemented in chrono::fea::ChInertiaCosseratMassref.

◆ SetMassPerUnitLength()

virtual void chrono::fea::ChInertiaCosseratAdvanced::SetMassPerUnitLength ( double mmu )

inlinevirtual

Set mass c, ex.SI units [kg/m].

Note that for uniform volumetric density \( \rho \), and area \( A \), this is also \( \mu = \rho A \).

The documentation for this class was generated from the following files:

/builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.h
/builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.cpp

Description

Public Member Functions

Additional Inherited Members

Constructor & Destructor Documentation

◆ ChInertiaCosseratAdvanced() [1/2]

◆ ChInertiaCosseratAdvanced() [2/2]

Member Function Documentation

◆ ComputeInertiaDampingMatrix()

◆ ComputeInertiaStiffnessMatrix()

◆ ComputeQuadraticTerms()

◆ GetInertiaJxxPerUnitLength()

◆ GetInertiaJyzPerUnitLength()

◆ GetMainInertiasInMassReference()

◆ SetInertiasPerUnitLength()

◆ SetMainInertiasInMassReference()

◆ SetMassPerUnitLength()