Description
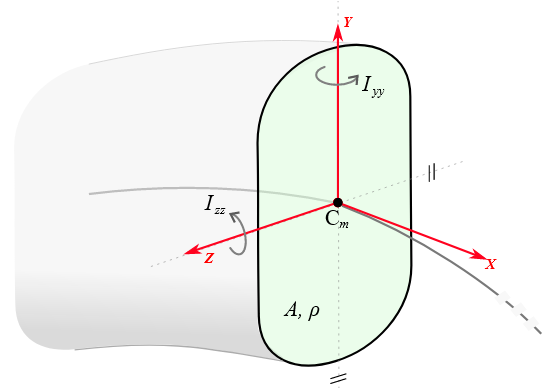
Inertia properties of a beam of Cosserat type, defined from an uniform density [kg/m^3], and the following geometric information:
- a section area
- Iyy Izz second moments of area The polar moment of area is automatically inferred via perpendicular axis theorem, Ip=Iyy+Izz. The section is assumed aligned to principal axis of the moment of area tensor, ie. Iyz=0, The section is assumed to be centered in the center of mass, The density is constant.
#include <ChBeamSectionCosserat.h>
Public Member Functions | |
| ChInertiaCosseratSimple (double density, double Area, double Iyy_area_moment, double Izz_area_moment) | |
| virtual void | ComputeInertiaMatrix (ChMatrix66d &Mi) override |
| Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mi]{xvel,wvel} The matrix is computed in the material reference (i.e. More... | |
| virtual void | ComputeInertiaDampingMatrix (ChMatrix66d &Ri, const ChVector3d &mW) override |
| Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference, i.e. More... | |
| virtual void | ComputeInertiaStiffnessMatrix (ChMatrix66d &Ki, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc) override |
| Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference. More... | |
| virtual void | ComputeQuadraticTerms (ChVector3d &mF, ChVector3d &mT, const ChVector3d &mW) override |
| Compute the values of inertial torque depending on quadratic velocity terms, per unit length, that is the gyroscopic torque w x [J]w . More... | |
| virtual double | GetMassPerUnitLength () override |
| Compute mass per unit length, ex.SI units [kg/m] In this case is simply \( \mu = \rho A \), given area in [m^2] and with \( \rho \) density in [kg/m^3]. | |
| virtual double | GetInertiaJxxPerUnitLength () |
| Compute the Jxx component of the inertia tensor per unit length, i.e. More... | |
| virtual double | GetInertiaJyyPerUnitLength () |
| Compute the Jyy component of the inertia tensor per unit length, i.e. More... | |
| virtual double | GetInertiaJzzPerUnitLength () |
| Compute the Jzz component of the inertia tensor per unit length, i.e. More... | |
| void | SetDensity (const double md) |
| Set the volumetric density, assumed constant in the section. Ex. SI units: [kg/m^3]. | |
| double | GetDensity () const |
| void | SetArea (const double ma) |
| Set the area of section for computing mass properties. Ex. SI units: [m^2]. | |
| double | GetArea () const |
| void | SetIyy (double mi) |
| Set the Iyy second moment of area of the beam (for bending about y in xz plane), defined as \( I_{yy} = \int_\Omega z^2 d\Omega \). More... | |
| double | GetIyy () const |
| void | SetIzz (double mi) |
| Set the Izz second moment of area of the beam (for bending about z in xy plane), defined as \( I_{zz} = \int_\Omega y^2 d\Omega \). More... | |
| double | GetIzz () const |
| virtual void | SetAsRectangularSection (double width_y, double width_z, double density) |
| Shortcut: set Izz, Iyy, Area and density at once, given the y and z widths of the beam assumed with rectangular shape, and volumetric density. More... | |
| virtual void | SetAsCircularSection (double diameter, double density) |
| Shortcut: set Izz, Iyy, Area and density at once, given the diameter the beam assumed with circular shape, and volumetric density. More... | |
 Public Member Functions inherited from chrono::fea::ChInertiaCosserat Public Member Functions inherited from chrono::fea::ChInertiaCosserat | |
| virtual void | ComputeInertialForce (ChVector3d &mFi, ChVector3d &mTi, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc) |
| Compute the total inertial wrench, ie forces and torques (per unit length). More... | |
Additional Inherited Members | |
 Public Attributes inherited from chrono::fea::ChInertiaCosserat Public Attributes inherited from chrono::fea::ChInertiaCosserat | |
| ChBeamSectionCosserat * | section |
| bool | compute_inertia_damping_matrix = true |
| Flag that turns on/off the computation of the [Ri] 'gyroscopic' inertial damping matrix. More... | |
| bool | compute_inertia_stiffness_matrix = true |
| Flag that turns on/off the computation of the [Ki] inertial stiffness matrix. More... | |
| bool | compute_Ri_Ki_by_num_diff = false |
| Flag for computing the Ri and Ki matrices via numerical differentiation even if an analytical expression is provided. More... | |
Constructor & Destructor Documentation
◆ ChInertiaCosseratSimple()
|
inline |
- Parameters
-
density the density fo the material [kg/m^3], assumed constant Area area of the section, [m^2] Iyy_area_moment second moment of area [m^4] about Y Izz_area_moment second moment of area [m^4] about Z
Member Function Documentation
◆ ComputeInertiaDampingMatrix()
|
overridevirtual |
Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference, i.e.
both linear and rotational coords assumed in the basis of the centerline reference.
- Parameters
-
Ri 6x6 sectional inertial-damping (gyroscopic damping) matrix values here mW current angular velocity of section, in material frame
Reimplemented from chrono::fea::ChInertiaCosserat.
◆ ComputeInertiaMatrix()
|
overridevirtual |
Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mi]{xvel,wvel} The matrix is computed in the material reference (i.e.
it is the sectional mass matrix). In this case it is simply a constant diagonal mass matrix with diagonal {rho*A,rho*A,rho*A, rho*Iyy+Izz, rho*Iyy, rho*Izz}
- Parameters
-
Mi 6x6 sectional mass matrix values here
Implements chrono::fea::ChInertiaCosserat.
◆ ComputeInertiaStiffnessMatrix()
|
overridevirtual |
Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference.
NOTE the matrix already contains the 'geometric' stiffness, so it transforms to absolute transl/local rot just like [Mi] and [Ri]: [Ki]_al =[R,0;0,I]*[Ki^]*[R',0;0,I'] , with [Ki^]=([Ki]+[0,f~';0,0]) for f=current force part of inertial forces.
- Parameters
-
Ki 6x6 sectional inertial-stiffness matrix [Ki^] values here mWvel current angular velocity of section, in material frame mWacc current angular acceleration of section, in material frame mXacc current acceleration of section, in material frame (not absolute!)
Reimplemented from chrono::fea::ChInertiaCosserat.
◆ ComputeQuadraticTerms()
|
overridevirtual |
Compute the values of inertial torque depending on quadratic velocity terms, per unit length, that is the gyroscopic torque w x [J]w .
Quadratic force is null as mass is centered. All terms expressed in the material reference, ie. the reference in the centerline of the section.
- Parameters
-
mF centrifugal term (if any) returned here mT gyroscopic term returned here mW current angular velocity of section, in material frame
Implements chrono::fea::ChInertiaCosserat.
◆ GetInertiaJxxPerUnitLength()
|
inlinevirtual |
Compute the Jxx component of the inertia tensor per unit length, i.e.
the part associated with rotation about the beam direction. In this case it is \( J_{xx} = \rho I_p \), where \( I_p = I_{zz} + I_{yy} \) is the polar moment of area.
◆ GetInertiaJyyPerUnitLength()
|
inlinevirtual |
Compute the Jyy component of the inertia tensor per unit length, i.e.
the part associated with rotation of the section on its Y axis. Defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), with \( \rho \) density in [kg/m^3]. For uniform density it is \( J_{yy} = \rho I_{yy} \), where \( I_{yy} = \int_\Omega z^2 d\Omega \) is the second moment of area.
◆ GetInertiaJzzPerUnitLength()
|
inlinevirtual |
Compute the Jzz component of the inertia tensor per unit length, i.e.
the part associated with rotation of the section on its Z axis. Defined as: \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), with \( \rho \) density in [kg/m^3]. For uniform density it is \( J_{zz} = \rho I_{zz} \), where \( I_{zz} = \int_\Omega y^2 d\Omega \) is the second moment of area.
◆ SetAsCircularSection()
|
virtual |
Shortcut: set Izz, Iyy, Area and density at once, given the diameter the beam assumed with circular shape, and volumetric density.
Assuming centered section.
◆ SetAsRectangularSection()
|
virtual |
Shortcut: set Izz, Iyy, Area and density at once, given the y and z widths of the beam assumed with rectangular shape, and volumetric density.
Assuming centered section.
◆ SetIyy()
|
inline |
Set the Iyy second moment of area of the beam (for bending about y in xz plane), defined as \( I_{yy} = \int_\Omega z^2 d\Omega \).
Note: some textbook calls this Iyy as Iy. Note: it can correspond to the same Iyy that you used for the elasticity, ex. in ChElasticityCosseratSimple. Ex. SI units: [m^4]
◆ SetIzz()
|
inline |
Set the Izz second moment of area of the beam (for bending about z in xy plane), defined as \( I_{zz} = \int_\Omega y^2 d\Omega \).
Note: some textbook calls this Izz as Iz. Note: it can correspond to the same Izz that you used for the elasticity, ex. in ChElasticityCosseratSimple. Ex. SI units: [m^4]
The documentation for this class was generated from the following files:
- /builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.h
- /builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.cpp
