Description
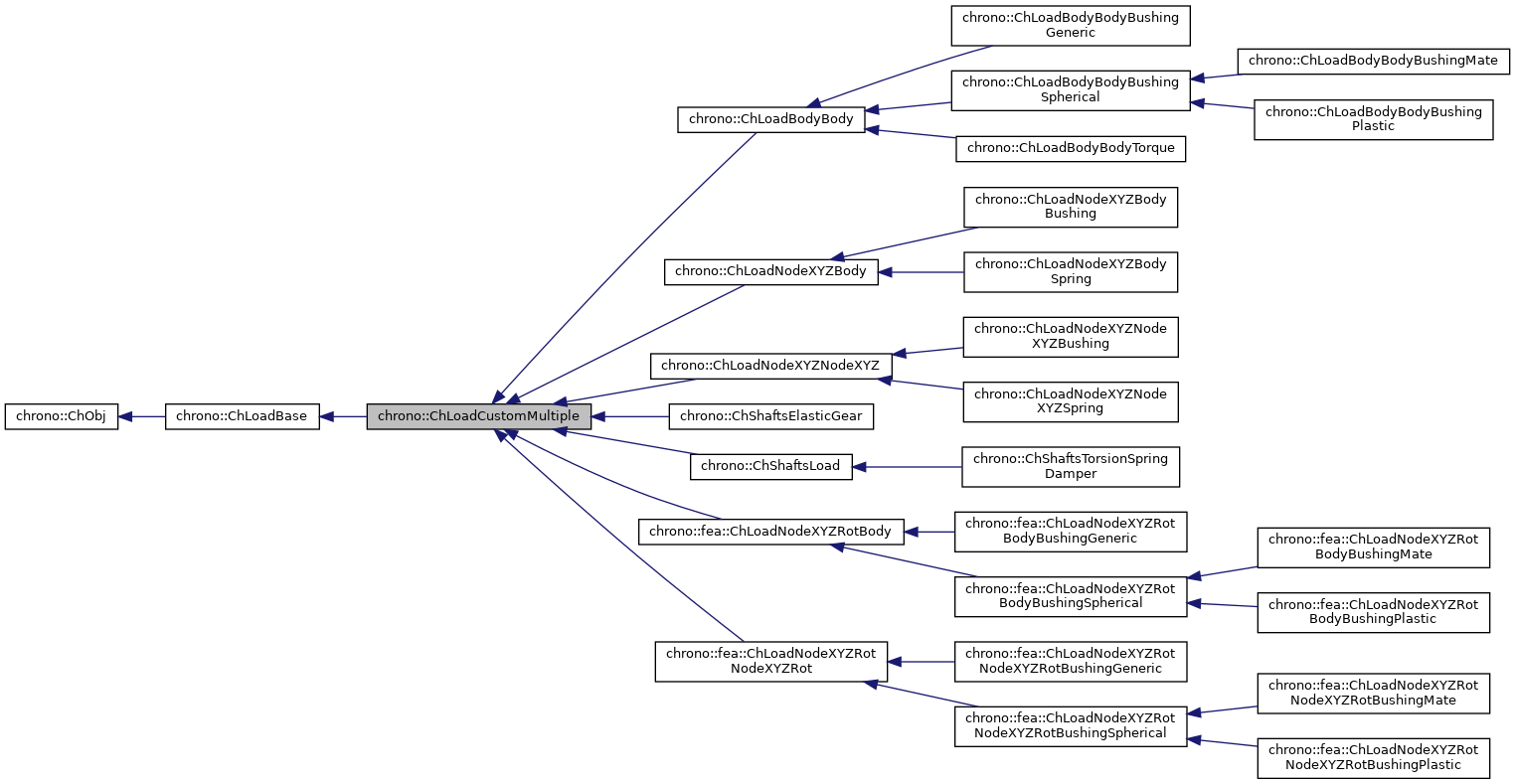
Loads acting on multiple ChLoadable items.
One must inherit from this and implement ComputeQ() directly. The ComputeQ() must write the generalized forces Q into the "load_Q" vector of this object. Given that multiple ChLoadable objects are referenced here, their sub-forces Q are assumed appended in sequence in the "load_Q" vector, in the same order that has been used in the std::vector "mloadables" for ChLoadCustomMultiple creation. The same applies for the order of the sub-matrices of in the Jacobian matrices K, R, M.
#include <ChLoad.h>
Public Member Functions | |
| ChLoadCustomMultiple (std::vector< std::shared_ptr< ChLoadable >> &loadable_objects) | |
| ChLoadCustomMultiple (std::shared_ptr< ChLoadable > loadableA, std::shared_ptr< ChLoadable > loadableB) | |
| ChLoadCustomMultiple (std::shared_ptr< ChLoadable > loadableA, std::shared_ptr< ChLoadable > loadableB, std::shared_ptr< ChLoadable > loadableC) | |
| virtual int | LoadGetNumCoordsPosLevel () override |
| Gets the number of DOFs affected by this load (position part). | |
| virtual int | LoadGetNumCoordsVelLevel () override |
| Gets the number of DOFs affected by this load (speed part). | |
| virtual void | LoadGetStateBlock_x (ChState &mD) override |
| Gets all the current DOFs packed in a single vector (position part). | |
| virtual void | LoadGetStateBlock_w (ChStateDelta &mD) override |
| Gets all the current DOFs packed in a single vector (speed part). | |
| virtual void | LoadStateIncrement (const ChState &x, const ChStateDelta &dw, ChState &x_new) override |
| Increment a packed state (e.g., as obtained by LoadGetStateBlock_x()) by a given packed state-delta. More... | |
| virtual int | LoadGetNumFieldCoords () override |
| Number of coordinates in the interpolated field. More... | |
| virtual void | ComputeJacobian (ChState *state_x, ChStateDelta *state_w) override |
| Compute Jacobian matrices K=-dQ/dx, R=-dQ/dv, and M=-dQ/da. More... | |
| virtual void | LoadIntLoadResidual_F (ChVectorDynamic<> &R, double c) override |
| Add the internal loads Q (pasted at global offsets) into a global vector R, multiplied by a scaling factor c. More... | |
| virtual void | LoadIntLoadResidual_Mv (ChVectorDynamic<> &R, const ChVectorDynamic<> &w, double c) override |
| Increment a vector R with the matrix-vector product M*w, scaled by the factor c. More... | |
| virtual void | LoadIntLoadLumpedMass_Md (ChVectorDynamic<> &Md, double &err, const double c) override |
| Add the lumped mass to an Md vector, representing a mass diagonal matrix. More... | |
| virtual void | CreateJacobianMatrices () override |
| Create the Jacobian loads if needed and set the ChVariables referenced by the sparse KRM block. | |
| virtual ChVectorDynamic & | GetQ () |
| Access the generalized load vector Q. | |
 Public Member Functions inherited from chrono::ChLoadBase Public Member Functions inherited from chrono::ChLoadBase | |
| virtual void | ComputeQ (ChState *state_x, ChStateDelta *state_w)=0 |
| Compute the generalized load(s). More... | |
| ChLoadJacobians * | GetJacobians () |
| Access the Jacobians (if any, i.e. if this is a stiff load). | |
| virtual void | Update (double time, bool update_assets) override |
| Update, called at least at each time step. More... | |
| virtual bool | IsStiff ()=0 |
| Report if this is load is stiff. More... | |
| virtual void | InjectKRMMatrices (ChSystemDescriptor &descriptor) |
| Register with the given system descriptor any ChKRMBlock objects associated with this item. | |
| virtual void | LoadKRMMatrices (double Kfactor, double Rfactor, double Mfactor) |
| Compute and load current stiffnes (K), damping (R), and mass (M) matrices in encapsulated ChKRMBlock objects. More... | |
 Public Member Functions inherited from chrono::ChObj Public Member Functions inherited from chrono::ChObj | |
| ChObj (const ChObj &other) | |
| virtual ChObj * | Clone () const =0 |
| "Virtual" copy constructor. | |
| int | GetIdentifier () const |
| Get the unique integer identifier of this object. More... | |
| void | SetTag (int tag) |
| Set an object integer tag (default: -1). More... | |
| int | GetTag () const |
| Get the tag of this object. | |
| void | SetName (const std::string &myname) |
| Set the name of this object. | |
| const std::string & | GetName () const |
| Get the name of this object. | |
| double | GetChTime () const |
| Gets the simulation time of this object. | |
| void | SetChTime (double m_time) |
| Sets the simulation time of this object. | |
| void | AddVisualModel (std::shared_ptr< ChVisualModel > model) |
| Add an (optional) visualization model. More... | |
| std::shared_ptr< ChVisualModel > | GetVisualModel () const |
| Access the visualization model (if any). More... | |
| void | AddVisualShape (std::shared_ptr< ChVisualShape > shape, const ChFrame<> &frame=ChFrame<>()) |
| Add the specified visual shape to the visualization model. More... | |
| std::shared_ptr< ChVisualShape > | GetVisualShape (unsigned int i) const |
| Access the specified visualization shape in the visualization model (if any). More... | |
| void | AddVisualShapeFEA (std::shared_ptr< ChVisualShapeFEA > shapeFEA) |
| Add the specified FEA visualization object to the visualization model. More... | |
| std::shared_ptr< ChVisualShapeFEA > | GetVisualShapeFEA (unsigned int i) const |
| Access the specified FEA visualization object in the visualization model (if any). More... | |
| virtual ChFrame | GetVisualModelFrame (unsigned int nclone=0) const |
| Get the reference frame (expressed in and relative to the absolute frame) of the visual model. More... | |
| virtual unsigned int | GetNumVisualModelClones () const |
| Return the number of clones of the visual model associated with this object. More... | |
| void | AddCamera (std::shared_ptr< ChCamera > camera) |
| Attach a camera to this object. More... | |
| std::vector< std::shared_ptr< ChCamera > > | GetCameras () const |
| Get the set of cameras attached to this object. | |
| void | UpdateVisualModel () |
| Utility function to update only the associated visual assets (if any). | |
| virtual void | ArchiveOut (ChArchiveOut &archive_out) |
| Method to allow serialization of transient data to archives. | |
| virtual void | ArchiveIn (ChArchiveIn &archive_in) |
| Method to allow de-serialization of transient data from archives. | |
| virtual std::string & | ArchiveContainerName () |
Public Attributes | |
| std::vector< std::shared_ptr< ChLoadable > > | loadables |
| ChVectorDynamic | load_Q |
Additional Inherited Members | |
 Protected Member Functions inherited from chrono::ChObj Protected Member Functions inherited from chrono::ChObj | |
| int | GenerateUniqueIdentifier () |
 Protected Attributes inherited from chrono::ChLoadBase Protected Attributes inherited from chrono::ChLoadBase | |
| ChLoadJacobians * | m_jacobians |
 Protected Attributes inherited from chrono::ChObj Protected Attributes inherited from chrono::ChObj | |
| double | ChTime |
| object simulation time | |
| std::string | m_name |
| object name | |
| int | m_identifier |
| object unique identifier | |
| int | m_tag |
| user-supplied tag | |
| std::shared_ptr< ChVisualModelInstance > | vis_model_instance |
| instantiated visualization model | |
| std::vector< std::shared_ptr< ChCamera > > | cameras |
| set of cameras | |
Member Function Documentation
◆ ComputeJacobian()
|
overridevirtual |
Compute Jacobian matrices K=-dQ/dx, R=-dQ/dv, and M=-dQ/da.
This default implementation uses finite differences for computing the K, R, M matrices if the load is stiff. If possible, a derived class should provide analytical Jacobians. Note: Given that multiple ChLoadable objects are referenced here, sub-matrices of K and R are pasted in (i,j) block positions that reflect the order in which loadable objects were specified.
- Parameters
-
state_x state position to evaluate Jacobians state_w state speed to evaluate Jacobians
Implements chrono::ChLoadBase.
◆ LoadGetNumFieldCoords()
|
overridevirtual |
Number of coordinates in the interpolated field.
For example, 3 for a tetrahedron finite element or a cable, 1 for a thermal problem, etc.
Implements chrono::ChLoadBase.
◆ LoadIntLoadLumpedMass_Md()
|
overridevirtual |
Add the lumped mass to an Md vector, representing a mass diagonal matrix.
In other words, perform the operation: Md += c*diag(M). Used by lumped explicit integrators. If mass lumping is impossible or approximate, adds scalar error to "err" parameter. If no mass matrix M is present (i.e., no inertial effects), implement as no-op. This default implementation uses the computed Jacobians (if available) to extract M = -dQ/da and then calculates Md += c*diag(M). A derived class should override this method if an analytical expressions for c*M*w is available.
- Parameters
-
Md result: Md vector, diagonal of the lumped mass matrix err result: not touched if lumping does not introduce errors c a scaling factor
Implements chrono::ChLoadBase.
◆ LoadIntLoadResidual_F()
|
overridevirtual |
Add the internal loads Q (pasted at global offsets) into a global vector R, multiplied by a scaling factor c.
In other words, perform the operation: R += forces * c
Implements chrono::ChLoadBase.
◆ LoadIntLoadResidual_Mv()
|
overridevirtual |
Increment a vector R with the matrix-vector product M*w, scaled by the factor c.
In other words, perform the operation: R += c*M*w (i.e., R += c*(-dQ/da)*w). If no mass matrix M is present (i.e., no inertial effects), implement as no-op. This default implementation uses the computed Jacobians (if available) to extract M = -dQ/da and then calculates R += c*M*w. A derived class should override this method if an analytical expressions for c*M*w is available.
- Parameters
-
R result: the R residual, R += c*M*w w the w vector c scaling factor
Implements chrono::ChLoadBase.
◆ LoadStateIncrement()
|
overridevirtual |
Increment a packed state (e.g., as obtained by LoadGetStateBlock_x()) by a given packed state-delta.
Compute: x_new = x + dw. This method is used in calculating Jacobians with finite difference approximations (default implementations of ComputeJacobian).
Implements chrono::ChLoadBase.
The documentation for this class was generated from the following files:
- /builds/uwsbel/chrono/src/chrono/physics/ChLoad.h
- /builds/uwsbel/chrono/src/chrono/physics/ChLoad.cpp
